Сумма внутренних углов четырехугольника - важная геометрическая характеристика, необходимая для решения различных математических задач. Рассмотрим методы определения этой величины для разных типов четырехугольников.
Содержание
Основная теорема о сумме углов
Для любого выпуклого четырехугольника сумма внутренних углов равна 360 градусам. Это правило работает независимо от формы четырехугольника, если он не имеет самопересечений.
Доказательство теоремы
- Проведите диагональ в четырехугольнике, разделяющую его на два треугольника
- Сумма углов каждого треугольника равна 180 градусам
- Сложите суммы углов двух треугольников: 180° + 180° = 360°
- Таким образом, сумма углов четырехугольника составляет 360 градусов
Особые случаи для различных четырехугольников
| Тип четырехугольника | Сумма углов | Дополнительные свойства |
| Прямоугольник | 360° | Все углы по 90° |
| Квадрат | 360° | Все углы по 90°, все стороны равны |
| Параллелограмм | 360° | Противоположные углы равны |
| Ромб | 360° | Противоположные углы равны, все стороны равны |
| Трапеция | 360° | Сумма углов при боковой стороне 180° |
Практические методы вычисления
Если известны три угла
- Сложите значения трех известных углов
- Вычтите полученную сумму из 360°
- Результат будет равен четвертому углу
Формула для n-угольника
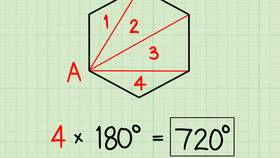
Общая формула суммы внутренних углов выпуклого n-угольника: S = (n-2) × 180°, где n - количество сторон. Для четырехугольника (n=4): S = (4-2) × 180° = 360°.
Примеры решения задач
| Условие | Решение |
| Найти четвертый угол, если три угла равны 80°, 90° и 110° | 80° + 90° + 110° = 280°; 360° - 280° = 80° |
| Все углы четырехугольника равны. Найти величину угла | 360° / 4 = 90° |
Применение в геометрических задачах
- Определение типа четырехугольника
- Решение задач на построение
- Доказательство теорем о четырехугольниках
- Вычисление неизвестных параметров фигуры
Проверка правильности вычислений
- Сумма всех углов должна равняться 360°
- В параллелограмме противоположные углы равны
- В прямоугольнике все углы прямые
- В равнобедренной трапеции углы при основании равны
Знание суммы углов четырехугольника и методов ее вычисления является фундаментальным для решения широкого круга геометрических задач. Это правило применяется как в теоретических доказательствах, так и в практических расчетах.