В математике и геометрии вопрос о "сумме" треугольника и квадрата может рассматриваться с различных точек зрения. Рассмотрим основные интерпретации этого понятия.
Содержание
В математике и геометрии вопрос о "сумме" треугольника и квадрата может рассматриваться с различных точек зрения. Рассмотрим основные интерпретации этого понятия.
Алгебраическая интерпретация
Если рассматривать треугольные и квадратные числа как элементы числовых последовательностей:
| Тип числа | Формула n-го элемента |
| Треугольное число (Tₙ) | n(n+1)/2 |
| Квадратное число (Kₙ) | n² |
Их сумма будет равна: Tₙ + Kₙ = n(n+1)/2 + n² = (3n² + n)/2
Геометрическая интерпретация
Площади фигур
Если рассматривать сумму как сложение площадей:
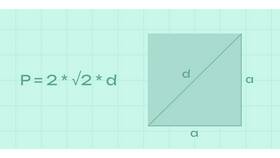
- Для треугольника со стороной a: SΔ = (a²√3)/4
- Для квадрата со стороной b: S□ = b²
- Сумма площадей: S = (a²√3)/4 + b²
Комбинация фигур
При объединении треугольника и квадрата возможны различные конфигурации:
- Квадрат с пристроенным треугольником
- Треугольник, вписанный в квадрат
- Фигуры, соединенные вершиной или стороной
Числовые примеры
| n | Треугольное число | Квадратное число | Сумма |
| 1 | 1 | 1 | 2 |
| 2 | 3 | 4 | 7 |
| 3 | 6 | 9 | 15 |
Практическое применение
Сумма этих понятий используется в:
- Комбинаторной геометрии
- Теории чисел
- Архитектурных расчетах
- Компьютерной графике
Заключение
Сумма треугольника и квадрата может рассматриваться как в числовом, так и в геометрическом смысле. В первом случае это алгебраическая сумма элементов последовательностей, во втором - комбинация геометрических свойств. Конкретное значение суммы зависит от выбранного контекста и параметров фигур.
